Motion

Motion

Motion is a fundamental concept in physics, encompassing the change in position of an object over time. This chapter delves into various types of motion, the equations that govern them, and the forces that influence them.

1. Types of Motion

Motion can be categorized based on the object’s path and its change in direction. Here, we explore three common types:

• Linear Motion:

• Involves an object moving along a straight line.
• The object’s displacement is a straight line segment from its starting point to its ending point.
• Examples: A car moving down a highway, a ball rolling on a straight track.

Circular Motion:

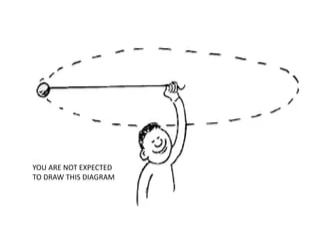
• An object traces a circular path around a fixed point (center of rotation).
• The object’s displacement is not a straight line, but rather the total distance traveled along the circular path (circumference).
• Examples: A merry-go-round rotating, a satellite orbiting Earth.

Projectile Motion:

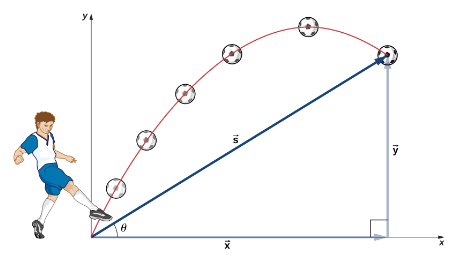
• A special case of linear and vertical motion combined.
• An object is launched at an angle with respect to the horizontal, influenced by gravity.
• The object follows a parabolic path.
• Examples: A ball thrown at an angle, a firework launched into the sky.

2. Equations of Motion

Understanding motion requires us to quantify its characteristics. Here, we introduce key concepts and their corresponding equations:

• Position (x): The location of an object at a specific time relative to a reference point. (Unit: meter [m])
• Displacement (Δx): The change in position of an object. It’s calculated as the final position (x_f) minus the initial position (x_i). (Unit: meter [m])
  • Δx = x_f – x_i
• Velocity (v): The rate of change of position with respect to time. It describes both the speed and direction of motion. (Unit: meter per second [m/s])
  • v = Δx / Δt (average velocity)
  • v = lim (Δt -> 0) Δx / Δt (instantaneous velocity)
• Acceleration (a): The rate of change of velocity with respect to time. It describes how quickly the object’s speed or direction is changing. (Unit: meter per second squared [m/s²])
  • a = Δv / Δt (average acceleration)
  • a = lim (Δt -> 0) Δv / Δt (instantaneous acceleration)

Kinematic Equations:

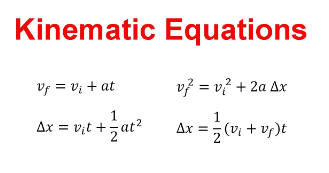
These equations relate the aforementioned quantities (position, displacement, velocity, acceleration, and time) under constant acceleration. They are powerful tools for analyzing various motion problems.

• v = u + at (relates velocity, initial velocity (u), acceleration, and time)
• Δx = ut + ½ at² (relates displacement, initial velocity, acceleration, and time)
• v² = u² + 2aΔx (relates final velocity, initial velocity, acceleration, and displacement)

Note: These equations assume constant acceleration. In real-world scenarios, acceleration might vary.

3. Forces Affecting Motion

Motion is not always spontaneous. Forces play a crucial role in initiating, stopping, or changing the motion of an object. Here, we explore two prominent forces:

Gravity:

• A fundamental force that attracts any two objects with mass.
• It acts towards the center of mass of the Earth (or any other massive object).
• Gravity is responsible for the weight of an object (the force exerted by gravity on the object).
• Near the Earth’s surface, the acceleration due to gravity (g) is approximately 9.8 m/s².

Friction:

• A force that opposes the relative motion between two surfaces in contact.
• It arises due to the microscopic irregularities on the surfaces that interlock and resist motion.
• There are different types of friction: kinetic friction (friction when objects are in motion), static friction (friction that prevents objects from moving), and rolling friction (friction associated with rolling objects).
• The magnitude of friction depends on the normal force (the force pressing the surfaces together) and the coefficient of friction (a material property that characterizes the frictional interaction).

Understanding how these forces interact with an object is essential for analyzing its motion. For instance, gravity pulls objects downwards, while friction opposes their movement. The net force acting on an object determines its acceleration according to Newton’s second law of motion (F = ma).